Prime Numbers.

Prime Number.

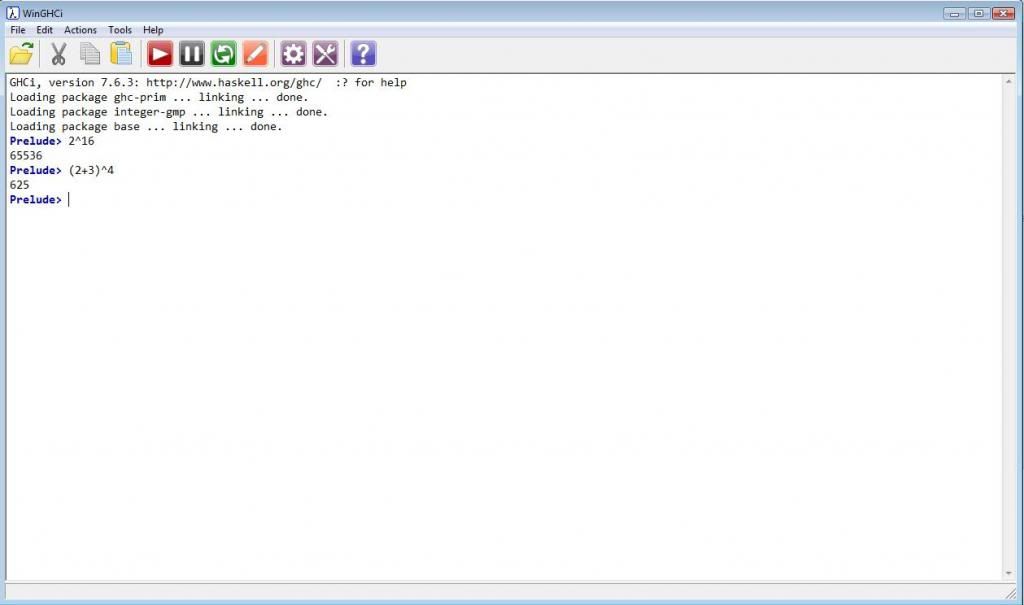
A 'Prime Number' is a natural number greater than 1 that has no proper divisors other than 1 and itself.

The Natural Numbers are 0, 1, 2, 3, 4, ....

The list of prime numbers starts with 2, 3, 5, 7, 11, 13, .... Except for 2, all of these are odd, of course.



Haskell Implementation for Prime Number Test.

1. Let's define divides function.

It should check if number m divides n, and this is true when and only when remainder of dividing n by m equals 0. The definition of divides function can therefore be phrased in terms of a predefined function rem for finding the remainder of a division process:


divides m n = ((rem n m) == 0)

in Haskell, symbol '=' is used for "is defined as" and symbol '==' for identity relation (and operator). Single apostrophes are used in this phrase only for showing terminal symbols boundaries. Terminal symbol is single "word" in "programming language", from which no other "words" can be produced, so it's not a "definition" or "production". For more details, please read Literature about languages and compilers.

A line of Haskell code of the form: foo t = .... (or: foo t1 t2 = .... , or: foo t1 t2 t3 = .... , and so on) is called a Haskell equation. In such an equation, foo is called the function and t its formal argument (or: t1 t2 t3 its formal arguments).

Thus, in the Haskell equation: divides m n = ((rem n m) == 0) , divides is the function, m is the first formal argument, and n is the second formal argument.


2. Let's test 'divides' function.

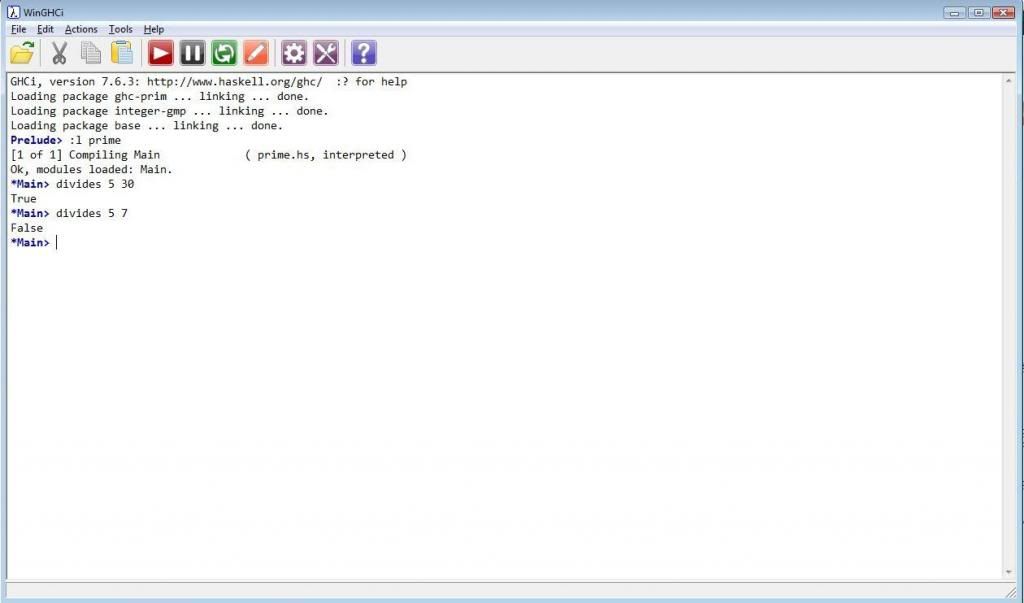
We can put definition of divides in a file: 'prime.hs'. After that we can start Haskell Interpreter and load that file in memory.

Prelude> :l prime

Then we can call it, to execute as follows:

*Main>divides 5 7

or

*Main>divides 5 30

When executed, it will be parsed, or converted into processor instructions and will return results 'immediately', without prior compilation needed. Because it's interpreted by Interpreter, instead of being compiled by Compiler.




3. Let's define & test 'ld' function.

'ld' stands for 'least divisor'.

For convenience we can define supporting function 'ldf' that finds least divisor (pl: 'dzielnik') of a dividend (pl: 'dzielna') n, starting from a given threshold (pl: 'próg') k, with k ≤ n.

This means we are to find least divisor of n, which is not less than k.


We have:


ld n = ldf 2 n

ldf k n | divides k n = k
          | k^2 > n = n
          | otherwise = ldf (k+1) n





(TODO: explain, nicely and precisely, what happens in above example, and how we can think about guarded equations, such as with 'ldf' function.)

(TODO: finish Haskell Implementation for Prime Number Test).

(Source: [1]).

Fern.

Barnsley's Fern.

for source code or image files click on a corresponding image in a Fractal gallery to the left side of this blog.


Barnsley's Fern.

The fern is one of the basic examples of self-similar sets, i.e. it is a mathematically generated pattern that can be reproducible at any magnification or reduction. Like the Sierpinski triangle, the Barnsley fern shows how graphically beautiful structures can be built from repetitive uses of mathematical formulas with computers.

Barnsley's book about fractals is based on the course which he taught for undergraduate and graduate students in the School of Mathematics, Georgia Institute of Technology, called Fractal Geometry. After publishing the book, a second course was developed, called Fractal Measure Theory. Barnsley's work has been a source of inspiration to graphic artists attempting to imitate nature with mathematical models.

The fern code developed by Barnsley is an example of an iterated function system (IFS) to create a fractal. He has used fractals to model a diverse range of phenomena in science and technology, but most specifically plant structures.

"IFSs provide models for certain plants, leaves, and ferns, by virtue of the self-similarity which often occurs in branching structures in nature. But nature also exhibits randomness and variation from one level to the next; no two ferns are exactly alike, and the branching fronds become leaves at a smaller scale. V-variable fractals allow for such randomness and variability across scales, while at the same time admitting a continuous dependence on parameters which facilitates geometrical modelling. These factors allow us to make the hybrid biological models..."

—Michael Barnsley.


Paint Tutorial.

Though Barnsley's fern could in theory be plotted by hand with a pen and graph paper, the number of iterations necessary runs into the tens of thousands, which makes use of a computer practically mandatory. Many different computer models of Barnsley's fern are popular with contemporary mathematicians. As long as the math is programmed correctly using Barnsley's matrix of constants, the same fern shape will be produced.

The first point is painted at the origin (x₀ = 0, y₀ = 0) and then the new points are painted as described by functions f1, f2, f3 and f4, each resulting from Bernsley's matrix of constants transformations. Which function to use in given iteration, is determined 'randomly', as based on probablity factor from Bernsley's matrix of constants.

f₁:

x_n+1 = 0
y_n+1 = 0.16*y_n

This coordinate transformation is chosen 1% of the time and just maps any point to a point in the first line segment at the base of the stem. This part of the figure is the first to be completed in during the course of iterations.

f₂:

x_n+1 = 0.85*x_n + 0.04*y_n
y_n+1 = −0.04*x_n + 0.85*y_n+1.6

This coordinate transformation is chosen 85% of the time and maps any points inside the leaflets.

f₃:

x_n+1 = 0.2*x_n − 0.26*y_n
y_n+1 = 0.23*x_n + 0.22*y_n + 1.6

This coordinate transformation is chosen 7% of the time and maps point inside the leaflet (or pinna) to a point across the stem (one side).

f₄:

x_n+1 = −0.15*x_n + 0.28*y_n
y_n+1 = 0.26*x_n + 0.24*y_n + 0.44

This coordinate transformation is chosen 7% of the time and maps point inside the leaflet (or pinna) to a point across the stem (other side).

The first coordinate transformation draws the stem. The second generates successive copies of the stem and bottom fronds to make the complete fern. The third draws the bottom frond on the left. The fourth draws the bottom frond on the right. The recursive nature of the IFS guarantees that the whole is a larger replica of each frond. Note that the complete fern is within the range −2.1820 < x < 2.6558 and 0 ≤ y < 9.9983.

(Source).

Critic is requested and welcome.

Fractals.

def. 'Fractal is a figure or surface generated by successive subdivisions of a simpler polygon or polyhedron, according to some iterative process'.

(Source).

Haskell interpreter exercise.

Simple Expressions exercise.


Haskell interpreter can be downloaded from Haskell home page.

When executed, it looks like this:



Haskell Interpreter WinGHCi.

The string 'Prelude>' is the Haskell prompt.

Haskell interpreter can be used as calculator, as follows:



WinGHCi used as Calculator.

In this blog we won't teach any programming language though, except for explaining basics needed to understand exercises.

(Source: [1]).

Tools Used.

Haskell Language.

Java 8 Language (early access for now).

Processing Language.

Introduction.

What is 'Paradigm' ?

According to me it's 'The Way of Perceiving' from which 'The Way of Thinking' emerges.

For example there can be 'Functional Programming Paradigm', 'Object Oriented Programming Paradigm', 'Medieval Paradigm', 'Modern Paradigm', 'Historical Paradigm', 'Eastern Philosophy Paradigm' etc....

What is 'Programming Paradigm' ?

A programming paradigm is a fundamental style of computer programming, a way of building the structure and elements of computer programs.

There are four main paradigms: imperative, functional, object-oriented, and logic programming.

i think i've discovered 'Objectional' Programming Paradigm, that is... partly Object-Oriented, partly Functional ;) .

Functional Programming Paradigm.

In computer science, functional programming is a programming paradigm, a style of building the structure and elements of computer programs, that treats computation as the evaluation of mathematical functions and avoids state and mutable data. Functional programming emphasizes functions that produce results that depend only on their inputs and not on the program state - i.e. pure mathematical functions. It is a declarative programming paradigm, which means programming is done with expressions. In functional code, the output value of a function depends only on the arguments that are input to the function, so calling a function f twice with the same value for an argument x will produce the same result f(x) both times. Eliminating side effects, i.e. changes in state that don't depend on the function inputs, can make it much easier to understand and predict the behavior of a program, which is one of the key motivations for the development of functional programming.

Functional programming has its roots in lambda calculus, a formal system developed in the 1930s to investigate computability, the Entscheidungsproblem, function definition, function application, and recursion. Many functional programming languages can be viewed as elaborations on the lambda calculus, where computation is treated as the evaluation of mathematical functions and avoids state and mutable data.

In contrast, imperative programming changes state with commands in the source language, the most simple example is the assignment. Functions do exist, not in the mathematical sense, but the sense of subroutine. They can have side effects that may change the value of program state. Functions without return value therefore make sense. Because of this, they lack referential transparency, i.e. the same language expression can result in different values at different times depending on the state of the executing program. (because functions also depend on state or context, not only on function arguments).

Why it's worth to hire paradigmatists as programmers?

They can solve problems very well, for they can understand other person's viewpoint.

For paradigmatists solving problem using different computational model, paradigm, or idea is easier. Judging from my programming experience, main problem with professional programming is teamwork and understanding other people's ideas anyway (i think that everyone thinks little differently, perhaps except from Buddhas).

Mathematics.

i think Mathematics is important part of Programming, especially Functional Programming.

This blog will contain articles related with Mathematics & articles related with Functional Programming as well.


See also, if You wish: Paradigms & Programming Languages.